Математический нейрон Маккалока — Питтса, формальный нейрон — узел искусственной нейронной сети, являющийся упрощённой моделью естественного нейрона.
Математический, искусственный нейрон обычно представляют как некую нелинейную функцию от единственного аргумента — линейной композиции всех входных сигналов. Данную функцию именуют функцией активации либо функцией срабатывания, передаточной функцией. Приобретенный итог посылается на единственный выход. Такие искусственные нейроны объединяют в сети — соединяют выходы одних нейронов с входами других.
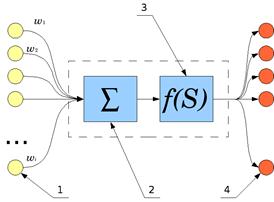

Рис. 12.5 Схема искусственного нейрона
1 – Примыкающие нейроны, выходные сигналы которых поступают на вход данному нейрону. 2 — Сумматор входных сигналов. 3 — Вычислитель передаточной функции. 4 — Нейроны, на входы которых подаётся выходной сигнал данного нейрона. 5 — wi — веса входных сигналов.
Математическая модель искусственного нейрона была предложена У. Маккалоком и В. Питтсом совместно с моделью сети, состоящей из этих нейронов. Создатели проявили, что сеть на таких элементах может делать числовые и логические операции. Фактически сеть была реализована Фрэнком Розенблаттом в 1958 году как компьютерная программка, а в последствии как электрическое устройство — перцептрон (перцепция переводится как чувствительность, потому перцептрон – сенсорная система).
Сначала нейрон мог оперировать только с сигналами логического нуля и логической единицы, так как был построен на базе био макета, который может пребывать исключительно в 2-ух состояниях — возбужденном либо невозбужденном.
Развитие нейронных сетей показало, что для расширения области их внедрения нужно, чтоб нейрон мог работать не только лишь с бинарными, да и с непрерывными (аналоговыми) сигналами. Такое обобщение модели нейрона было изготовлено Уидроу и Хоффом, которые предложили в качестве функции срабатывания нейрона использовать логистическую кривую.
Связи, по которым выходные сигналы одних нейронов поступают на входы других, нередко именуют синапсами по аналогии со связями меж био нейронами. Любая связь характеризуется своим весом. Связи с положительным весом именуются возбуждающими, а с отрицательным — тормозящими. Нейрон имеет один выход, нередко именуемый аксоном по аналогии с биологическим макетом. С единственного выхода нейрона сигнал может поступать на случайное число входов других нейронов.
Математически нейрон представляет собой сумматор, единственный выход которого определяется через его входы и матрицу весов последующим образом:
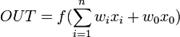
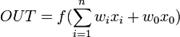
тут 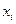
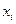
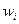
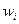
Вероятные значения сигналов на входах нейрона всегда лежат в интервале [0,1], они могут быть или дискретными (нуль либо единица), или аналоговыми. Дополнительный вход 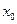
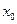
Передаточная функция определяет зависимость сигнала на выходе нейрона от взвешенной суммы сигналов на его входах. Почти всегда она является однообразно растущей и имеет область значений [-1,1] либо [0,1], но есть исключения. Также для неких алгоритмов обучения сети нужно, чтоб она была безпрерывно дифференцируемой на всей числовой оси. Искусственный нейрон стопроцентно характеризуется собственной передаточной функцией. Внедрение разных передаточных функций позволяет заносить нелинейность в работу нейрона и в целом нейронной сети.
В главном, нейроны систематизируют на базе их положения в топологии сети. Делят:
- Входные нейроны — принимают начальный вектор, кодирующий входной сигнал. Обычно, эти нейроны не делают вычислительных операций, а просто передают приобретенный входной сигнал на выход, может быть, усилив либо ослабив его.
- Выходные нейроны — представляют собой выходы сети. В выходных нейронах могут выполняться какие-либо вычислительные операции.
- Промежные нейроны — делают главные вычислительные операции.
Главные типы передаточных функций нейрона:
- линейная функция активации с насыщением;
- линейная передаточная функция.
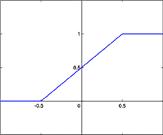

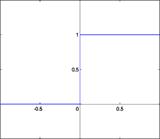

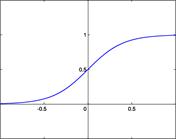

Рис. 12.6 Разновидности передаточных функций нейронов (линейная, пороговая, сигмоидальная).
Сигнал на выходе нейрона линейно связан с взвешенной суммой сигналов на его входе. В искусственных нейронных сетях со слоистой структурой нейроны с передаточными функциями такового типа, обычно, составляют входной слой. Не считая обычный линейной функции могут быть применены её модификации.
Недочетами шаговой и полулинейной активационных функций относительно линейной можно именовать то, что они не являются дифференцируемыми на всей числовой оси, а означает, не могут быть применены при обучении по неким методам.
Пороговая передаточная функция представляет собой перепад. До того времени пока взвешенный сигнал на входе нейрона не добивается некого уровня — сигнал на выходе равен нулю. Как сигнал на входе нейрона превосходит обозначенный уровень — выходной сигнал скачкообразно меняется на единицу.
Самый 1-ый представитель слоистых искусственных нейронных сетей — перцептрон состоял только из нейронов такового типа. Ввиду того, что данная функция не является дифференцируемой на всей оси абсцисс, её нельзя использовать в сетях, обучающихся по методу оборотного распространения ошибки и другим методам, требующим дифференцируемости передаточной функции.
Сигмоидальная передаточная функция – один из самых нередко применяемых, сейчас, типов передаточных функций. Введение функций сигмоидального типа было обосновано ограниченностью нейронных сетей с пороговой функцией активации нейронов. При таковой функции активации хоть какой из выходов сети равен, или нулю, или единице, что ограничивает внедрение сетей. Внедрение сигмоидальных функций позволило перейти от бинарных выходов нейрона к аналоговым. Функции передачи такового типа, обычно, присущи нейронам, находящимся во внутренних слоях нейронной сети.
Логистическая функция. Математически эту функцию можно выразить так:
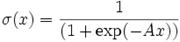
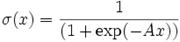
Тут A — это параметр функции, определяющий её крутизну. Когда A стремится к бесконечности, функция вырождается в пороговую. При A = 0 сигмоида вырождается в постоянную функцию со значением 0,5. Область значений данной функции находится в интервале (0,1). Принципиальным достоинством этой функции является простота её производной:
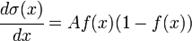
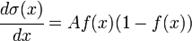
То, что производная этой функции может быть выражена через её значение упрощает внедрение этой функции при обучении сети по методу оборотного распространения. Особенностью нейронов с таковой передаточной чертой будет то, что они усиливают сильные сигналы значительно меньше, чем слабенькие, так как области сильных сигналов соответствуют пологим участкам свойства. Это позволяет предупредить насыщение от огромных сигналов.
Вышеперечисленные функции составляют только часть от огромного количества передаточных функций, применяемых сейчас. В число других передаточных функций входят такие, как: экспонента f(x) = exp( — Ax); тригонометрический синус; модульная: 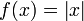
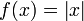
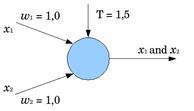

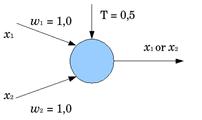

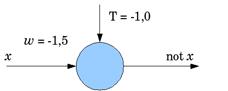

Рис. 12.7 Схемы нейронов,моделирующие логические функции: «И», «ИЛИ», «НЕ».
Изображения иллюстрируют, каким образом можно, задав веса входных сигналов и порог чувствительности, вынудить нейрон делать конъюнкцию (логическое «И») и дизъюнкцию (логическое «ИЛИ») над входными сигналами, также логическое отрицание входного сигнала. Этих 3-х операций довольно, чтоб смоделировать полностью всякую логическую функцию хоть какого числа аргументов.
Нейронные сети, построенные на искусственных нейронах, обнаруживают некие признаки, которые позволяют сделать предположение о сходстве их структуры со структурой мозга живых организмов. Все же, даже на низшем уровне искусственных нейронов есть значительные различия. К примеру, искусственный нейрон является безынерционной системой, другими словами сигнал на выходе возникает сразу с возникновением сигналов на входе, что совершенно нехарактерно для био нейрона.
