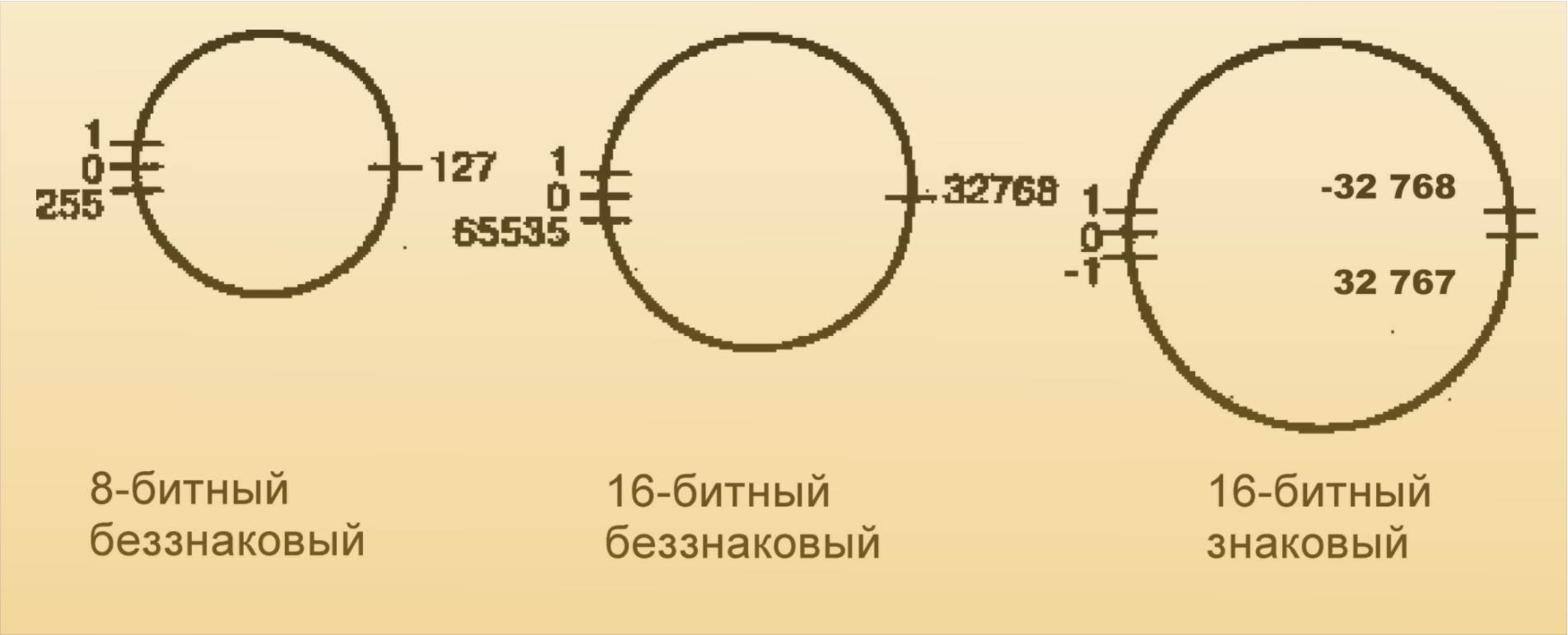
Наглядным представлением любого целого типа данных является кольцо, состоящее из расположенных по порядку констант этого типа, причем рядом с максимальным значением в типе находится минимальное, например:
Результатом прибавления единицы в арифметике c фиксированным количеством разрядов является следующее по часовой стрелке за исходным число в кольце, а результатом вычитания единицы — следующее число по ходу против часовой стрелки. Данный факт очевиден, кроме случаев перехода от максимально допустимого числа к минимальному при прибавлении единицы и от минимального к максимальному при вычитании.
Продемонстируем вышесказанное. Рассмотрим вначале беззнаковые типы. Максимально допустимое число в k-разрядном беззнаковом типе равно 2k -1 и состоит из k-1 единиц. При прибавлении к такому числу единицы получаем 2k, что соответствует нулю в k-разрядной арифметике.
Вычитание из нуля единицы соответствует прибавлению к нулю минус единицы. По правилам k-разрядной арифметики, минус единица — это дополнение единицы до 2k, то есть число, которое при сложении с единицей даст 2k. Очевидно, что таковым является число 2k -1, состоящее из k двоичных единиц. Значит, в беззнаковых типах 0 + (-1) = 2k — 1, что и равно максимальному значению в типе.
Операции сложения, вычитания и умножения в k-битных беззнаковых типах соответствуют математическому понятию арифметические операции по модулю 2k (сравнение по модулю 2k).
В знаковых k-разрядных типах максимально допустимым является число 2k-1-1 (k-1 двоичная единица). При увеличении такого числа на 1 мы получаем 2k-1 или единицу в знаковом бите и нули в остальных, что соответствует отрицательному числу с максимально возможным модулем.