Если подумать, то может показаться странным, что кинетическая энергия при упругих столкновениях, оставаясь одной и той же до и после столкновения, должна изменяться в процессе самого столкновения. Например, при столкновении двух одинаковых частиц, сближающихся с равными скоростями, существует момент времени, когда обе частицы полностью останавливаются (момент времени, разделяющий сближение и разлет частиц), и кинетическая энергия системы обращается в нуль, как бы совсем исчезая.

В отличие от кинетической энергии импульс системы остается постоянным до, во время и после столкновения. Конечно, ниоткуда не следует, что кинетическая энергия тоже должна оставаться постоянной, однако факт ее исчезновения и появления естественным образом подводит нас к вопросу: не существует ли нечто такое, что нарастает при уменьшении кинетической энергии, причем сумма кинетической энергии и этого нечто остается в течение всего столкновения постоянной?

Оказывается, что это нечто существует, и в случае сил, величина и направление которых зависят лишь от положения частиц системы,-оно развивается в понятие, применимость которого выходит далеко за рамки проблемы столкновений, и настолько мощное, что оно определяет развитие будущих разделов физики и сохраняется даже тогда, когда механика в форме Ньютона уже неприменима. Это понятие называется потенциальной энергией. Это очень удачное название, так как вызывает у человека верные ассоциации. Понятие кинетической энергии, которую можно было бы назвать энергией движения, весьма наглядно, потому что оно связано со скоростью частицы. Понятие же потенциальной энергии, связанное с определенной внутренней структурой системы, менее наглядно, но оно характеризует способность (потенцию) превращения ее в энергию кинетическую.

Легче всего представить потенциальную энергию, если сравнить ее с запасенной энергией, которая способна переходить в энергию движения. За примерами далеко ходить не надо. Сжатая пружина обладает потенциальной энергией, которая переходит в энергию движения, если пружину освободить. Можно сказать, что поднятый на некоторую высоту груз тоже содержит потенциальную энергию в том смысле, что, если его отпустить, он начнет падать и будет набирать кинетическую энергию.

Начнем наши поиски потенциальной энергии с нахождения такой величины, которая остается постоянной во время движения, даже если кинетическая энергия при этом изменяется. Эту величину можно найти с помощью теоремы 11.3:

W_а→b (работа, произведенная над телом, при его перемещении из точки α в точку b) = изменению кинетической энергии тела—кинетической энергии в точке b минус кинетическая энергия в точке α=Т_b—Т_α. 

Величина, которая остается постоянной в процессе движения, получается из этого равенства путем совершенно тривиальной, на первый взгляд, перестановки слагаемых:

Т_а = Т_b – W_а→b,              (12.1)

Это соотношение означает, что начальная кинетическая энергия равна конечной энергии за вычетом работы, произведенной над телом. Начальная кинетическая энергия не зависит от последующего движения, поэтому она не изменяется в процессе движения. Это и есть та величина, которая остается постоянной.

Нельзя ли в таком случае определить разность потенциальных энергий как отрицательную работу, произведенную над телом? Оказывается, это можно сделать, не вводя при этом никаких ограничений на природу сил. Например, мы не обязаны ограничиваться силами, величина и направление которых зависят только от положения тел в системе, или силами, которые подчиняются третьему закону Ньютона. Таким образом, подобное определение возможно даже тогда, когда кинетическая энергия до столкновения не равна кинетической энергии после столкновения.

Представим брусок, скользящий по столу. Предположим, что его начальная кинетическая энергия равнялась Т_а. Сила трения, действующая между столом и бруском, замедляет его движение до тех пор, пока он не остановится, так что конечное значение кинетической энергии равно нулю. Из приведенной выше общей теоремы следует, что работа, произведенная над телом, равна начальной кинетической энергии со знаком «минус»:

Та = – W_а→b,   (12.2)

причем Т_а, разумеется, является постоянной величиной (фиг. 123).

Все эти рассуждения представляются весьма правдоподобными. Однако определенная указанным образом разность потенциальных энергий фактически необратима (во всяком случае, в том смысле, как нам этого хотелось бы) и не допускает никаких дальнейших интересных обобщений. Брусок, остановившись на столе, продолжает покоиться. Тем не менее можно обеспечить способность потенциальной энергии восстанавливаться и превращаться в кинетическую энергию, если ограничиться рассмотрением сил, аналогичных силам, действующим при упругих столкновениях, т. е. зависящих только от положения тела. Тем самым мы исключим случаи, подобные рассмотренному выше, где сила, останавливающая брусок, всегда направлена против его движения. Когда брусок останавливается, сила исчезает и не появляется до тех пор, пока мы снова не начнем его двигать. Если бы сила, действующая на брусок, зависела только от его положения, она продолжала бы действовать и после остановки бруска, возвращая его в исходное положение с начальной кинетической энергией. Укажем, например, на поведение того же бруска на идеально гладком столе под действием постоянной силы, зависящей только от его положения. Такой опыт можно осуществить с помощью системы, показанной на фиг. 124.

В качестве другого примера исследуем движение частицы, вертикально подброшенной вблизи земной поверхности. Движение частицы вверх замедляется под действием постоянной силы тяжести, которая удовлетворяет тому условию, что она зависит только от положения частицы¹. (Сила тяжести, будучи простейшим примером таких сил, постоянна как по величине, так и по направлению.) В отличие от силы трения она не изменяет своего направления при изменении направления движения частицы.

В данном случае зависимость от положения тривиальная, т. е. нет никакой зависимой. Важно, чтобы сила не зависела от каких-либо других факторов, например, от направления движения.

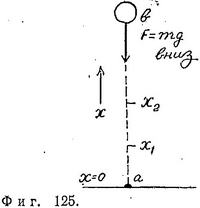
Предположим, что частица подброшена вверх из точки α (фиг. 125) с начальной кинетической энергией Т_а. Работа, совершенная силой тяжести над частицей при подъеме с нулевой высоты до высоты х, равна — mgx. Когда эта работа (взятая с обратным знаком) оказывается равной начальной кинетической энергии, частица останавливается:

mgx = Т_а.         (12.3)

Следовательно, максимальная высота подъема:

b = T_α/mg.              (12.4)

Достигнув максимальной высоты и остановившись, частица не повисает в воздухе. Она начинает падать и, когда долетает до Земли, набирает такое же количество кинетической энергии, какое у нее было вначале. Направление движения, однако, изменилось на противоположное. Таким образом, кинетическая энергия, уменьшавшаяся при движении частицы вверх, увеличивается при ее движении вниз. И когда частица возвращается в исходное положение, ее кинетическая энергия полностью восстанавливается. Подобная возможность восстановления кинетической энергии и придает смысл понятию потенциальной энергии.

Определим разность потенциальных энергий [см. уравнение (12.1)] как отрицательную работу, произведенную над телом при перемещении его из одной точки в другую, но будем считать, что это определение справедливо лишь тогда, когда силы зависят только от положения, поскольку именно для этого класса сил понятие потенциальной энергии приобретает особую ценность.

Определение. Разность потенциальных энергий в точках α и b =— работе, произведенной над телом при перемещении его из точки α в точку b.

При указанных условиях кинетическая энергия, теряемая телом, может вновь восполняться, и при этом можно говорить о сохранении полной энергии. По этой причине силы, зависящие только от положения, называются консервативными силами. Это такие силы, под действием которых механическая энергия сохраняется, подобно тому, как консервативным в политике считается тот, кто хранит традиции прошлого.

В качестве иллюстрации снова рассмотрим поведение частицы, находящейся под действием силы земного притяжения. Разность ее потенциальных энергий в точках х₁ и х₂ равна:

— работе, совершенной над частицей

при перемещении ее из х₁ в х₂ = — (— mg) (х₂—x₁) = mgx₂—mgх₁.

Подставляя (12.5) в (12.1) и раскрывая выражения для кинетической энергии, получаем:

Предположим, что частица была подброшена с поверхности Земли со скоростью v₀. В этом случае х₁=0, и (12.6) записывается в виде:

Таким образом, скорость v оказывается зависящей только от положения частицы. Можно, например, спросить: какое расстояние пройдет частица до остановки и начала падения? На максимальной высоте скорость частицы обращается в нуль (v=0). Поэтому:

или

На этой высоте скорость, а, следовательно, и кинетическая энергия частицы равны нулю. Потенциальная же энергия частицы достигает здесь своего максимального значения, причем оно равно по величине начальному значению кинетической энергии, что легко показать с помощью полученных уравнений:

Затем частица начинает падать и со временем достигает поверхности Земли. Непосредственно перед ударом о Землю расстояние ее до поверхности обращается в нуль и скорость частицы достигает первоначального значения. Однако направление скорости в полете изменилось. Теперь частица движется вниз, а не вверх. Тем не менее этот факт не сказывается на величине кинетической энергии, которая пропорциональна квадрату скорости, т. е. не зависит от направления движения. В данном случае можно считать, что в процессе движения кинетическая энергия сначала переходит в потенциальную, а затем наоборот, причем их сумма всегда остается постоянной величиной.

Для систем, состоящих из многих частиц, подобные представления не всегда очевидны, Кинетическая энергия может перейти в потенциальную и остаться в. такой форме. Например, если забросить тело на какую-нибудь площадку, чтобы оно осталось на ней, кинетическая энергия тела перейдет в потенциальную; обратное же превращение не произойдет до тех пор, пока мы не столкнем тело с площадки.