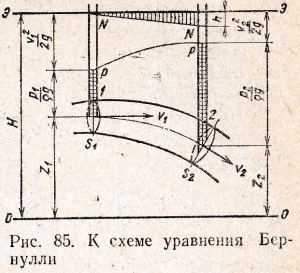
Основным уравнением гидродинамики, определяющим связь между давлением и скоростью в движущемся потоке жидкости, является уравнение Бернулли. Для двух произвольных поперечных живых сечений 1, 2 (рис. 85) элементарной струйки идеальной жидкости можно записать следующее уравнение энергетического баланса (м):
где Z — геометрический напор, высота положения частицы жидкости над плоскостью отсчета, м; p/pg — пьезометрический напор, представляющий собой полный запас потенциальной энергии 1 кг жидкости, м; υ2/2g — скоростной напор, представляющий собой 3 удельную кинетическую энергию 1 кг жидкости, м; Н — напор, м.
Таким образом, при установившемся движении идеальной жидкости для любого сечения справедливо уравнение:
Это уравнение называется уравнением Бернулли для элементарной струйки идеальной жидкости.
Уравнение Бернулли для потока реальной жидкости. Для потока реальной вязкой жидкости необходимо учитывать потери напора, на участке от первого до второго сечения потока, которые складываются из потерь на трение (линейные потерн) hЛ и потерь на местные сопротивления hМ (м):
hПОТ = hЛ + hМ
В практических расчетах учитывают различие в скоростях по сечению потока, при этом расчетное значение удельной кинетической энергии потока получается несколько меньше действительного. Это обстоятельство учитывается введением поправочного коэффициента α, определенного опытным путем. Тогда уравнение Бернулли для потока реальной жидкости записывают в следующем виде:
где α1 и α2 — коэффициенты Кориолиса.
Уравнение Бернулли является основным уравнением гидродинамики, в котором в математической форме записан закон сохранения энергии.