Рассмотренный пример заставил Макса Борна выдвинуть свою интерпретацию волновой функции, следствия которой оказались чрезвычайно далеко идущими. Позднее Борн писал:

«И снова руководящей явилась идея Эйнштейна. Он пытался сделать понятным дуализм частиц (квантов, или фотонов) и воли, интерпретируя квадрат амплитуд оптических волн как плотность вероятности появления фотонов. Эту идею можно было немедленно распространить на ψ-функцию: |ψ|² должна представлять плотность вероятности для электронов (или других частиц). Утверждать это было легко, но как это можно было доказать?».

В настоящее время вероятностная интерпретация волновой функции, развитая Борном, является общепринятой. Квадрат волновой функции ψ² характеризует плотность вероятности¹⁾. Частица с большей вероятностью находится в том месте, где ее волновая функция велика, и с меньшей вероятностью там, где ее волновая функция мала. Мы снова оперируем с ψ², а не с ψ, поскольку ψ может быть отрицательной величиной, а интерпретировать отрицательную вероятность весьма сложно. Из такой интерпретации вытекает требование, чтобы полная площадь под кривые зависимости ψ² от χ равнялась единице. Это требование означает, что электрон обязательно находится в каком-то месте пространства, а такое «событие» считается достоверным.

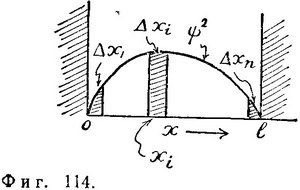
Снова рассмотрим случай, когда частица, заключенная между двумя абсолютно твердыми стенками, находится в основном состоянии (фиг. 114). Если считать ψ² плотностью вероятности, то вероятность нахождения частицы в интервале Δх_i равна:

ψ²(x_i)Δх_i

Вероятность нахождения частицы вблизи стенок мала, так как величина ψ² в этих местах тоже мала. Полная вероятность должна равняться единице (поскольку мы считаем, что частица обязательно находится где-то между этими стенками). Следовательно,

площадь под кривой «ψ²(x₁)Δх₁ + … + ψ²(x_n)Δх_n = 1.

Отсюда вытекает общее условие, согласующееся с вероятностной интерпретацией, что полная площадь под кривой равна единице.

1) Снова заметим: правильно говорить о квадрате только в том случае, когда волновая функция — действительное число. Мы рассматриваем только такие случаи.

Эксперимент с электроном, налетающим на препятствие, объясняется теперь следующим образом. Мы принимаем, что электрон начинает двигаться слева, и его волновая функция до соприкосновения с препятствием тоже находится слева. После столкновения с препятствием часть волновой функции отражается, а часть проходит через него. Квадрат прошедшей части волновой функции (волновой функции справа от препятствия), просуммированный по всей области справа, характеризует вероятность того, что электрон проник сквозь препятствие, а квадрат отраженной части волновой функции — вероятность того, что электрон отразился от него²⁾. На вопрос: попадет ли электрон в детектор? — мы отвечаем: вероятность попадания электрона в детектор равна площади той части, возведенной в квадрат волновой функции, которая прошла направо. Когда же электрон действительно попадает в детектор, то он обладает полной массой и полным зарядом.

Отдельный электрон может попасть в детектор, а может и не попасть. Если же в сторону препятствия движется большое количество электронов — либо эксперимент с единичным электроном повторяется многократно, либо в сторону препятствия было одновременно выпущено много электронов, — то картина, выглядевшая вначале случайной, будет становиться все более регулярной. Часть электронов пройдет через препятствие и попадет в детектор, остальные же отразятся. Но каждый из электронов будет нести полные массу и заряд.

Вероятностная интерпретация волновой функции исключает необъяснимое «расщепление» электрона па части. Однако мы теперь не в состоянии ни сказать, где в действительности находится электрон, ни предугадать, попадет или нет в детектор определенный электрон. Можно только утверждать, например, что вероятность попадания электрона в детектор равна одной пятой, вероятность же отражения его от препятствия — четырем пятым. Мы возражаем: «Но ведь это игра в рулетку. Неужели лучшего нельзя достигнуть?» Ответ на это возражение, согласующийся с квантовой теорией и вероятностной интерпретацией, однозначен: нет, лучшего достигнуть нельзя.

Подобно горной цепи, разделяющей континент на две части и питающей водой ту или иную его половину, вероятностная интерпретация отделяет квантовую теорию от всей физики, которая предшествовала ей. В классической теории, основы которой были заложены в работах Декарта и Ньютона, имели дело с движением осязаемых частиц — твердых, обладающих массой и неделимых, положение которых в пространстве всегда четко определено. Суть теории Ньютона состоит в следующем: если заданы положение и скорость частицы в какой-то момент времени и заданы силы, действующие на эту частицу, то положение частицы в любой последующий момент времени строго определено и всегда может быть вычислено. Классическим примером такого утверждения служит движение планет вокруг Солнца. Задаваясь силой тяготения и законами движения Ньютона, мы можем рассчитать орбиты планет для любого момента времени как в будущем, так и в прошлом. Можно предсказать затмение Солнца, которое случится через 25 столетий, т. е. найти особое взаимное расположение Земли, Луны и Солнца через 25 веков после момента вычисления, а можно установить и точное время затмения, происшедшего 25 веков назад. Используя результаты вычисления «обратного» движения планет и их спутников, можно устанавливать даты исторических событий.

2) Вероятность достоверного события равна по определению единице. Например, вероятность того, что при подбрасывании монеты выпадет орел или решка, равна единице. Вероятность выпадения орла равна 1/2, т. е. орел будет выпадать примерно в половине случаев. На столе для игры в рулетку имеется 37 чисел: 0, 1, …, 36. Вероятность остановки шарика у какой-то цифры равна 1/37, т. е. в одном из 37 случаев шарик остановится у этой цифры. Однако всякий, кто играл в рулетку, знает, что от этой цифры бывают отклонения в обе стороны.

Именно такую возможность для частиц и отрицает квантовая механика. Если бы Солнце, Луна и Земля вели себя как квантовые частицы (согласно современным представлениям они действительно так себя ведут, но величина квантовых эффектов для таких тел слишком мала, чтобы их можно было заметить), то единственное, что мы смогли бы сказать, это то, что вероятность затмения Солнца, т. е. особого взаимного расположения Солнца, Луны и Земли, которое произошло, скажем, 5 или 25 веков назад, равна либо одной трети, либо одной второй, либо одной четверти. Таким образом, точная дата затмения или исторического события становится неизвестной. Именно это обстоятельство вызывает наибольший протест. Нет никаких причин заранее считать, что все в мире можно предсказать с абсолютной определенностью или даже с некоторой вероятностью. Тем не менее представление о существовании законов, управляющих движением и носящих детерминированный характер, прочно укоренилось в нас; оно с успехом использовалось по крайней мере со времен Ньютона и подразумевалось во многих более ранних трудах. Новая идея пришлась многим не по душе. Эйнштейн возражал, говоря, что «бог не играет с миром в кости». Сам Шредингер так и не принял статистическую интерпретацию. Как-то он укорял Макса Борна за то, что тот продолжал утверждать, будто вероятностная интерпретация является общепринятой, хотя, по мнению Шредингера, с ней не согласны, помимо него самого, Эйнштейн, Планк, де Бройль и другие. («Ты знаешь, Макс, что я очень люблю тебя и ничто не может изменить это; тем не менее я должен устроить тебе основательную взбучку…»)

Самое удивительное в данной ситуации состоит в том, что сама волновая функция является полностью определенной. Если в какой-то момент времени заданы волновая функция системы и силы, действующие на нее, то с помощью уравнения Шредингера можно найти точный вид волновой функции в любой последующий момент времени. Все дело в том, что волновая функция, несущая согласно квантовой механике всю возможную информацию, не содержит в полной мере того, что мы привыкли ожидать. В результате нам кажется, что вместо реализации четко организованного плана мы вынуждены играть в лотерею. Но мы знаем, что математическая структура теории (соотношение между постулатами и теоремами или между самими теоремами) часто оказывается наиболее важным элементом этой теории. Случается, что интерпретация теории меняется, а структура ее соотношении и согласие с действительностью остаются прежними. Например, интерпретация механики Ньютона существенно изменилась за последние два столетия. Тем не менее структура ее соотношений, скажем соотношения между гравитационной силой и параметрами эллиптической орбиты, осталась неизменной.