Найдем энтропию сложного опыта α ^ β в этом случае, если опыты не являются независящими, т.е. если на финал β влияет итог опыта α. К примеру, если в ящике всего два разноцветных шара и α состоит в извлечении первого, а β — второго из их, то а стопроцентно снимает неопределенность сложного опыта α ^ β, т.е. оказывается Н(α ^ β) = H(α), a не сумме энтропии, как надо из (2.5).

Связь меж α и β заключается в том, что какие-то из исходов A^(α) могут влиять на финалы из В^(β), т.е. некие пары событий A_i ^ B_j не являются независящими. Но тогда в (2.6) p(A_i ^ B_j) следует подменять не произведением вероятностей, а, согласно (А.14):

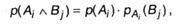
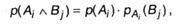
где — р_Ai (B_j) возможность пришествия финала В, при условии, что в первом опыте имел место финал А_i.

Тогда

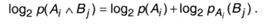
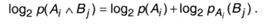
При подстановке в (2.6) получаем:

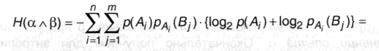
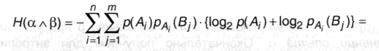
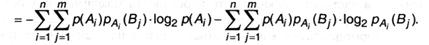
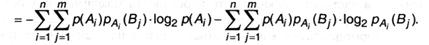
В первом слагаемом индекс j имеется только у B; изменив порядок суммирования, получим члены вида:

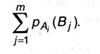
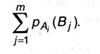
Но,

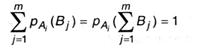
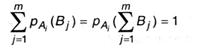
так как

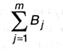
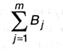
образует достоверное событие (какой-нибудь из исходов опыта β все равно реализуется). Как следует, 1-ое слагаемое оказывается равным:

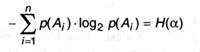
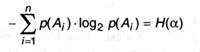
Во 2-м слагаемом члены вида

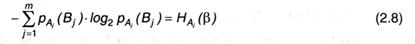
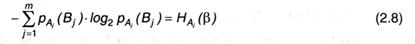
имеют смысл энтропии опыта β при условии, что в опыте а реализовался финал А_i — будем именовать ее условной энтропией. Если ввести данное понятие и использовать его обозначение, то 2-ое слагаемое будет иметь вид:

где H_α(β) есть средняя условная энтропия опыта β при условии выполнении опыта α. Совсем получаем для энтропии сложного опыта:

Приобретенное выражение представляет собой общепринятое правило нахождения энтропии сложного опыта. Совсем разумеется, что выражение (2.5) является личным случаем (2.10) при условии независимости опытов α и β.

Относительно условной энтропии можно высказать последующие утверждения:

1. Условная энтропия является величиной неотрицательной. H_α(β) = 0 исключительно в том случае, если хоть какой финал а стопроцентно определяет финал β (как в примере с 2-мя шарами), т.е.

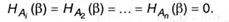
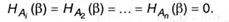
В данном случае Н(α ^ β) = Н(α).

2. Если опыты α и β независимы, то Н_α(β) = Н(β), при этом это оказывается большим значением условной энтропии. Другими словами, опыт α не может повысить неопределенность опыта β; он может или не оказать никакого воздействия (если опыты независимы), или снизить энтропию β.

Приведенные утверждения можно соединить одним неравенством:

т.е. условная энтропия не превосходит бесспорную.

3. Из соотношений (2.10) и (2.11) следует, что

при этом равенство реализуется исключительно в том случае, если опыты α и β независимы.