Проанализируем теперь механическое представление о свете, используя основные положения механики Ньютона, которые не были известны Декарту, но вполне отвечали его идеям. Декарт предположил, что свет является объектом, подобным теннисному мячу и обладающим свойством инерции, так что в однородной среде (воздухе, вакууме, воде) он движется с постоянной скоростью до тех пор, пока на него не подействует какая-то сила. На границе двух сред или на поверхности отражателя действуют силы, которые 1) изменяют скорость объекта от- начального до конечного значения на величину, не зависящую от угла падения, и 2) не изменяют тангенциальную (касательную) компоненту скорости объекта. Можно ли придумать силу, которая бы действовала на границе раздела двух сред подобным образом?
Если предположить, что сила направлена по нормали к границе, то горизонтальная компонента скорости останется, согласно второму закону, неизменной. Чтобы конечная скорость частицы не зависела от угла падения, изменение ее кинетической энергии (конечная кинетическая энергия минус начальная) тоже не должно зависеть от этого угла. Используя теорему 11.3 (изменение кинетической энергии равно произведенной работе), можно заключить, что произведенная над теннисным мячом работа не должна зависеть от угла падения.
В качестве механической модели, обладающей требуемыми силовыми свойствами, можно предложить две горизонтальные расположенные друг под другом плоские поверхности. Первая (лежащая выше) поверхность соединяется со второй с помощью наклонной плоскости. Работа, производимая над скатывающимся по наклонной плоскости шаром, не зависит от угла, под которым он движется относительно верхней плоскости. Поэтому изменение кинетической энергии шара будет всегда одним и тем же. Вместе с тем сила, действующая на шар, не имеет горизонтальной компоненты. Следовательно, такая модель, предложенная еще Ньютоном и представленная на фото 19, обладает всеми требуемыми свойствами.
Преломление
Шар, перемещаясь по верхней плоскости, обладает скоростью v1 его угол падения равен θi, а потенциальная энергия равна mgh. 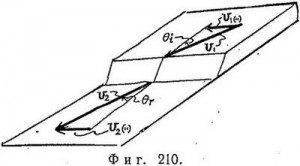

На нижней плоскости его скорость равна v2, угол преломления — θr. и потенциальная энергия — нулю. Тогда: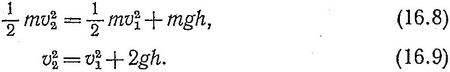
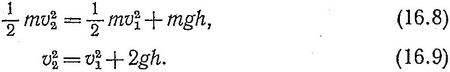
Составляющая скорости, параллельная границе, остается неизменной:![]()
![]()
Поэтому:![]()
![]()
В результате отношение синусов равно:![]()
![]()
и не зависит от углов.
Если считать свет подобным теннисному мячу, становится понятным его прямолинейное и равномерное движение в свободном пространстве. Вводя дополнительные допущения о характере сил, действующих на границе двух сред, можно объяснить явления отражения п преломления света. Далее, с помощью новых, вполне резонных предположений можно понять поглощение и прохождение света. Если теннисные мячи поглощаются средой, разумно допустить, что они передают свое движение среде, тем самым нагревая ее. Если же они проходят через нее, они уносят движение с собой, нагревая среду меньше или вовсе не нагревая ее. Так, солнечный свет сильнее нагревает темную поглощающую поверхность, чем стеклянную поверхность, а снег под темным пятном тает быстрее, чем окружающий его чистый снег. Мы можем предвидеть также, что свет, ударяясь об отражающую поверхность и отскакивая от нее, действует на поверхность с силой, равной той силе, с которой поверхность отражает свет. Эта сила, как нетрудно догадаться, чрезвычайно мала, однако ее величину все же удалось измерить. Оказалось, что она не столь уж ничтожна, чтобы отвергнуть, как бессмысленное, предложение использовать в будущем давление солнечного света для того, чтобы подгонять огромные «парусные» космические корабли в открытом пространстве солнечной системы.
Остается разрешить только несколько проблем. Франческо Гримальди обнаружил, что свет не всегда распространяется прямолинейно даже в однородной среде. Он писал:
«Свет распространяется и рассеивается не только по прямой линии, испытывая преломление и отражение, но и посредством дифракции».
Гримальди нашел, что свет, проходящий через небольшое отверстие и затемненную комнату, образует на стене изображение, размеры которого превосходят размеры изображения, получившегося, если бы спет распространялся прямолинейно:
«…особенно следует отметить, что пятно… оказывается значительно больше, чем в случае, если бы свет распространялся прямолинейно».
Это явление, однако, без особых натяжек можно согласовать с корпускулярной теорией, если допустить, что между частицами света, входящего в затемненную комнату, и краем отверстия действуют некие слабые силы, притягивающие частицы к краю и тем самым расширяющие изображение.


Гораздо более серьезное затруднение возникает при попытке объяснить открытое Ньютоном явление, известное под названием колец Ньютона. Если осветить сверху два куска стекла, имеющих определенные формы, как показано на фиг. 211, то получается круговое изображение, состоящее из темного пятна в центре, окруженного темными концентрическими кольцами. Это явление заставило Ньютона связать со светом некую волну. Он писал:
«При падении света на тонкую пленку или пластинку какого-нибудь прозрачного тела волны, возбужденные прохождением света через первую поверхность, обгоняют лучи один за другим. Когда луч дойдет до второй поверхности, то волны заставят его там отразиться или преломиться соответственно тому, какая часть волны обгоняет там луч, сгущенная или разреженная».
Волна, возбуждаемая частицей света на поверхности пластины, создает благоприятные «условия» либо для отражения, либо для прохождения света, в результате чего образуются темные кольца. Позднее Майкельсон заметил:
«Ньютоновское объяснение «цветов тонких пленок» в действительности оказалось неверным, однако следует учесть, что ему удалось измерить величину, известную теперь под названием длины волны, и показать, что каждому спектральному цвету соответствует определенная длина волны».
Таким образом, как уже было сказано, в корпускулярной теории света имелись определенные трудности, причем Ньютон уже располагал достаточной информацией для выдвижения волновой теории. Однако настоящие серьезные затруднения корпускулярной теории возникли позднее. Во времена Декарта и Ньютона удалось хорошо объяснить все известные явления в предположении, что свет обладает свойствами частиц. Правда, в некоторых случаях, особенно при объяснении колец Ньютона, приходилось вводить искусственные допущения, однако в целом теория выглядела вполне удовлетворительной.
Что же представляют собой частицы света? Безусловно, они не являются теннисными мячами, даже очень маленькими. В самом деле, два пучка света проходят один через другой без всякого видимого взаимодействия. Теннисные же мячи должны сталкиваться. Если бы свет был подобен теннисным мячам, то эти мячи должны были бы каким-то образом проникать друг сквозь друга или сталкиваться настолько редко, чтобы эти столкновения были несущественны. Обладает ли свет такими свойствами теннисных мячей, как жесткость или цвет? Каковы размеры и масса световых корпускул? Распространяется ли свет в виде дискретных порций? На последний вопрос Декарт, как и Ньютон, вероятно, ответил бы «да». Позднее ученые стали говорить «нет». А сейчас мы снова говорим «да». Свет, как недвусмысленно заявлял Декарт, обладает некоторыми свойствами теннисных мячей. Как и теннисный мяч, он распространяется прямолинейно в однородной среде. Подобно мячу, свет отражается от твердой гладкой поверхности. Как и теннисный мяч при правильно подобранных силах, свет преломляется при переходе из одной среды в другую и т. д. Для иллюстрации перечисленных явлений Декарт рассматривает настоящие теннисные мячи и ракетки, пренебрегая теми их свойствами, которые его не интересуют, — размером, формой, цветом и ворсистостью — и учитывая лишь те, которые ему нужны, — внутренние свойства, определяющие реакцию мяча на действие силы. Конечно, ни Декарт, ни его ученики никогда не считали, что свет состоит из «настоящих» крохотных теннисных мячей.
Благодаря огромному авторитету Ньютона его вера в то, что свет представляет собой поток частиц, приостановила, особенно в Англии, проверку других гипотез о природе света. Ньютону казалось маловероятным, что свет является волной, «так как волны огибают углы, и то время как для света это не наблюдается». Возможно, корпускулярная теория света была по душе Ньютону потому, что она соответствовала общей корпускулярной интерпретации окружающей природы. Материя, как можно было бы думать, состоит из частиц, движущихся в пустоте; казалось, что и свет следовало бы рассматривать подобным образом. Однако известно, что Ньютон очень не любил выдвигать какие-либо гипотезы. Например, он писал:
«Следует отметить, что доктрина, использовавшаяся мной при объяснении преломления и цветов, включает лишь определенные свойства света и не содержит гипотез, объясняющих эти свойства, … ибо гипотезы полезны только для объяснения свойств вещей, а не для определения их, по крайней мере, поскольку свойства могут быть установлены опытами».
И далее:
«Это верно, что из моей теории я заключаю о телесности света, но делаю это безо всякой решительной настойчивости… Но я знал, что утверждаемые мною свойства света могут быть в некоторой степени объяснены не только этой, но и многими другими механическими гипотезами».
Ньютон не дал никакой интерпретации природы тяготения:
«Вы иногда говорите о тяготении, как о чем-то неотъемлемом и присущем материи. Умоляю, не приписывайте мне таких знаний, поскольку я не претендую познать источник тяготения, для чего потребуется гораздо больше времени» (из письма к Бентли).
И снова в Поучении в конце «Начал»:
«Довольно того, что тяготение на самом деле существует и действует согласно изложенным нами законам, и вполне достаточно для объяснения всех движений небесных тел и моря».
Ньютон старался оставить открытыми вопросы об источнике гравитации и о природе света. Его коллеги и современники пытались заставить его дать объяснение этих вещей. Однако он предпочитал не делать этого. Введение гравитационной силы, предположение, что свет является потоком частиц, приводили к результатам, согласующимся с экспериментом. Ньютон стремился именно к этому. Поэтому вряд ли можно заподозрить раздражение во фразе, которую он написал в конце своих «Начал»: «hypotheses nonfingo» («гипотез не измышляю»).
