Как уже было сказано, для описания языка-объекта должен применяться метаязык. Но метаязык также должен владеть некими качествами формального языка, чтоб совершенно точно определять конструкции языка-объекта. Как следует, метаязык должен быть поначалу описан сам, зачем также нужен язык — естественно, может сложиться воспоминание, что таковой процесс никогда не завершится. Но подтверждено, что для описания хоть какого метаязыка можно использовать язык естественный. Таким образом, для построения формального языка нужно средствами естественного языка обрисовать метаязык, а потом средством метаязыка обрисовать язык формальный. Разглядим два варианта описания метаязыков.
Один из обширно всераспространенных метаязыков известен как нотации Бекуса-Наура. Для формирования предложений в форме Бекуса-Наура употребляются универсальные метасимволы: <, >, ::=, . 1-ые два метасимвола именуют «угловыми скобками» — они служат для обрамления нетерминального знака. Знак «::=» читается «по определению есть»; знак «|» — «или». В предложениях, записанных в форме Бекуса-Наура, нетерминальный знак, стоящий в угловых скобках, играет роль определяемой конструкции языка-объекта. В формулах Бекуса-Наура могут употребляться терминальные знаки из алфавита языка-объекта, хорошие от универсальных метасимволов. Терминальные знаки формального языка ничем не ограничиваются.
Описание формального языка строится из последовательности формул, любая из которых в левой части содержит один метасимвол, обозначающий некую конструкцию языка-объекта. Правая часть таковой формулы содержит или перечисление метасимволов и терминальных знаков языка-объекта (никаких разделителей при всем этом не ставится), или совокупы перечислений, разбитых эмблемой «|». Правая и левая части соединяются воединыжды в единую формулу знаком «::=».
Язык-объект можно считать стопроцентно определенным в форме Бекуса-Наура, если хоть какой нетерминальный знак можно представить последовательностью терминальных знаков.
В качестве примера можно разглядеть определение понятия «идентификатор», которое употребляется в почти всех языках программирования. На естественном языке определение звучит последующим образом: «Идентификатор — это неважно какая последовательность букв и цифр, начинающаяся с буквы». В форме Бекуса-Наура оно будет смотреться последующим образом:
<идентификатор>::=<буковка>/<идентификатор>< буковка> /<идентификатор>
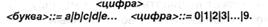
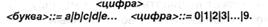
Видно, что в определении данного понятия находится рекурсивность, так как понятие «идентификатор» определяется через само себя. Простым оказывается идентификатор из одной буковкы.
Достоинство нотаций Бекуса-Наура в том, что они представляется в буквенном виде; неудобны нотации однообразностью методов построения предложений языка-объекта — запись оказывается массивной и плохо воспринимаемой.
Еще более приятной следует считать другой метод описания формального языка, предложеннный Никласом Виртом — создателем языка программирования PASCAL, получивший заглавие «синтаксические диаграммы». Синтаксическая диаграмма — это схема (графическое представление) описания какого-нибудь нетерминального знака языка-объекта. Схема всегда имеет один вход и один выход. Элементами схемы могут служить терминальные знаки языка-объекта, заключенные в окружность (либо овал) либо нетерминальные знаки (понятия) языка-объекта, заключенные в прямоугольник. Элементы соединяются меж собой направленными линиями, указывающие порядок следования объектов в определяемом нетерминальном знаке.
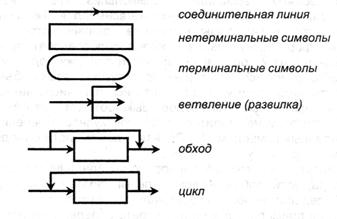

Структура синтаксических диаграмм схожа структурам языков программирования, что позволило обширно использовать диаграммы для написания трансляторов разных языков. Первым языком, описанным при помощи синтаксических диаграмм, был язык PASCAL.
Чтение диаграммы делается в направлении стрелок; в точке ветвления может выбираться хоть какой маршрут. В качестве метаязыка может употребляться естественный российский язык; языки программирования строятся на английской базе. Терминальные знаки переписываются в конструкции формального языка дословно. Нетерминальные знаки могут выражаться через терминальные либо другие нетерминальные — в данном случае для их строятся уточняющие диаграммы; в конечном счете, все нетерминальные знаки должны быть выражены через терминальные. При использовании синтаксических диаграмм принимается условие, что посреди терминальных знаков языка-объекта не должно быть схожих, также ни один из терминальных знаков не может служить началом другого. При нарушении данного условия может быть многозначное чтение диаграммы и, как следствие, построение либо определение неправильной конструкции языка.
Разглядим ряд примеров построения синтаксических диаграмм, первым из которых будет определение понятия «Идентификатор» для сравнения с приведенной выше нотацией Бекуса-Наура.
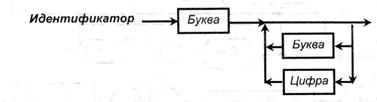

Нужны уточняющими диаграммы:
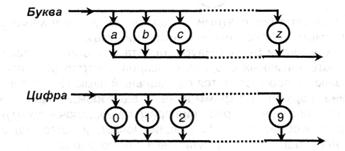

Примерами построения английских идентификаторов в согласовании с этой диаграммой являются: q, a 123, identificator, e2e4.
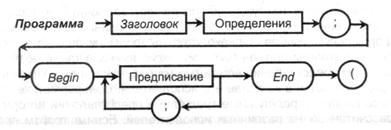
Диаграмма, задающая вид программки на языке PASCAL, смотрится последующим образом:

В качестве примеров предписаний разглядим условное и повторяющееся.
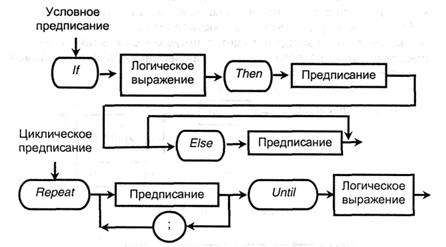

В согласовании с этими и схожими диаграммами строятся допустимые синтаксические конструкции языка.
Итак, нотации Бекуса-Наура и синтаксические диаграммы — это два других метода описания конструкций метаязыка, при помощи которого строится формальный язык. После того, как построена формальная грамматика, и ею порожден язык, он может быть применен для решения прикладных задач — коммуникации, хранения и обработки инфы. Последний класс задач приводит к необходимости формулировки при помощи языков последовательностей обработки инфы, т.е. алгоритмов, и их представлению в форме, доступной для осознания и выполнения лицом либо техническим устройством, которые обработку создают.
