Сложность современного уровня развития производства приводит к тому, что обслуживающий персонал не всегда способен вовремя и правильно оценить значимость сложившейся ненормальной ситуации либо проблемы в оборудовании. Это может привести к нарушению технологического процесса либо даже к появлению аварийных ситуаций. В неких случаях требуется обрабатывать и рассматривать информацию, поступающую от нескольких датчиков, при этом данные должны находиться в строго данных спектрах, которые зависят от результатов других измерений. Нередко датчики работают в экстремальных критериях, характеризующихся наличием сильных термических, механических и других неблагоприятных воздействий на чувствительные элементы измерительных преобразователей.
В связи с тем, что применяемые для этих целей датчики контроля в большинстве случаев выдают измерительную информацию с большой степенью неопределенности, как по вине самих измерительных устройств, так и из-за непостоянности контролируемого параметра, принятие решений может быть основано на использовании понятий нечеткой логики. Задачки подобного типа стимулировали развитие систем с искусственным умом, искусственных нейронных сетей.
При реализации в системах управления и регулирования сложных многофункциональных зависимостей будет нужно внедрение комбинированных регуляторов с процессорами, выполняющими большой объем вычислительных операций, что определит понижение быстродействия и надежность управления и регулирования в динамическом режиме работы. Для решения таких сложных задач управления и регулирования представляется многообещающим создание внедрение устройств контроля с нечеткой логикой, основанных на разработке и применении нелинейных многофункциональных преобразователей. К примеру, для целей автоматизации технологических процессов в энергетике, хим производстве лучшим решением может явиться внедрение контроллеров с нечеткой логикой.
Система принятия решений изредка нужна для того, чтоб выносить строгие решения типа «черное» либо «белое», почаще требуется более узкая оценка, типа «градации серого». Применение лингвистического подхода в арифметике (понятие неоднозначной логики) ввел польский ученый Ян Лукашевич в 1930 году. Логические переменные в ней могут принимать любые значения в промежутке меж 0 и 1. Значение, которое воспринимает величина, отражает степень вероятности ее истинности. При всем этом для свойства состояния объекта контроля употребляют понятие нечеткого огромного количества.
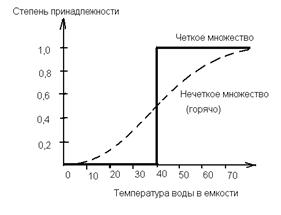

Рис. 12. 8 Черта состояния объекта контроля с внедрением понятий нечеткой логики.
После выполнения логических операций и оценки результатов от системы требуется выдать точный ответ. Для этого употребляют понятие центроида (центр массы тела в механике). В теории измерений этому понятию соответствует математическое ожидание значения измеряемой физической величины.
Функция принадлежности к нечеткому огромному количеству может быть введена в программку нечеткой логики и как непрерывная математическая функция. Для этого употребляют, к примеру, треугольную форму, гауссоиду (функция принадлежности соответствует понятию ЗРСВ). Программное обеспечение для систем с нечеткой логикой имеют такие функции в стандартных библиотеках. Разумеется, понятию степени принадлежности можно привести в соответствие понятие точности измерений, характеризующееся значением СКО результатов неоднократных измерений либо результатов, приобретенных от огромного числа первичных измерительных преобразователей.
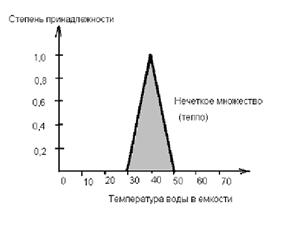

Рис. 12.9 Черта состояния объекта контроля с внедрением дополнительных градаций понятий нечеткой логики.
Модификаторы нечетких множеств (дополнительные градации) именуются хеджами. Существует математическая теория множеств, в каких употребляют логические операции: дополнения («не»), скрещения («и»); объединения («или»).
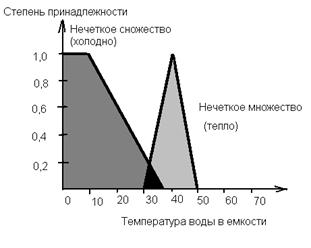

Рис. 12.10 Нечеткие огромного количества с внедрением операций скрещения и объединения.
Функция принадлежности для нечетких множеств задается профессионалом (фазификация). После выполнения логических операций и оценки результатов от системы требуется выдать точный ответ с внедрением, к примеру, понятия «центроида» (дефазификация).
Внедрение опыта и умения профессионалов в механизм функционирования устройств позволяет учесть нелинейность, преломления, непостоянность, деградацию датчиков. При всем этом нет необходимости в разработке серьезной математической модели объекта управления (правила и выводы можно изменять прямо во время работы устройства).
Область использования устройств с нечеткой логикой содержит в себе системы контроля с огромным спектром неопределенности контролируемых характеристик, для регулирования и управления процессами с быстроизменяющимися в широких границах параметрами. Настроечные коэффициенты непрерывных регуляторов (с разными законами регулирования) выбираются исходя из данных характеристик свойства регулирования объекта управления. САР рассчитывается как линейная для рабочего спектра конфигураций возмущения по заданию либо нагрузке. Но реальные объекты по собственной природе не линейны, потому рассчитанные опции регуляторов оптимальны исключительно в округах рабочей точки объекта, а при огромных отклонениях — не оптимальны.
