Отыскать значение функции f(3,2), если она задана последующими соотношениями:
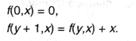
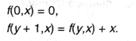
В этом случае g(х) = 0, h(x, y, z) = у + z. Потому что f(0, x) = g(х) = 0 при любом х, то и f(0,2) = 0, а другие значения можно вычислить поочередно:
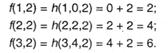
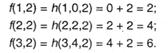
Нетрудно обосновать, что в данном примере f(x, y) = х ∙ у
Операция минимизации
Пусть задана некая функция f(x, y). Зафиксируем значение х и выясним, при каком у значение f(x, y) = 0. Более сложной оказывается задачка отыскания меньшего из числа тех значений у, при которых f(x,y) = 0. Так как итог решения таковой задачки, разумеется, находится в зависимости от х, то и меньшее у является функцией х. Примем обозначение:
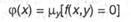
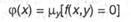
(читается: «наименьшее у такое, что f(x,y) = 0», а μy именуют μ-оператором либо оператором минимизации).
Схожим же образом определяется функция многих переменных:
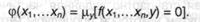
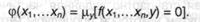
Для вычисления функции φ можно предложить последующую функцию:
- Вычисляем f(x1, …xn, 0); если значение равно нулю, то полагаем φ(х1,…хп) = 0. Если f(х1, xn, 0) ≠ 0, то перебегаем к последующему шагу.
- Вычисляем f(x1,…хп, 1); если значение равно нулю, то полагаем φ(х1,…хп) = 1. Если f(x1, хп, 0) ≠ 0, то перебегаем к последующему шагу и т.д.
Если окажется, что для всех у функция f(x1, …xn, 0) ≠ 0, то функция φ(х1,…хn) считается неопределенной.
