Энергия электрона Шредингера (с учетом спина) как функция импульса дается выражением:
E = p2/2m (47.9)
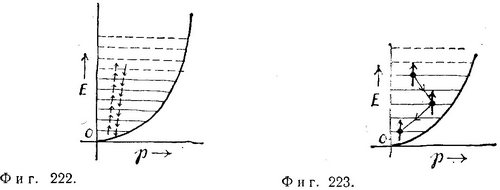
В случае, когда этот электрон заключен в сосуде, его уровни энергии дискретны и расположены довольно часто. На фиг. 222 изображены энергетические уровни электрона Шредингера, обладающего спином. Каждому уровню отвечают два спиновых состояния. Расстояние между нижним уровнем и осью абсцисс определяется принципом неопределенности (и зависит от размеров сосуда). На каждом из уровней могут одновременно находиться два электрона с противоположно направленными спинами. Согласно принципу запрета, каждой волне де Бройля могут соответствовать не более двух электронов. Если электрон Шредингера, первоначально находившийся в каком-то состоянии с импульсом р и энергией Е, сталкивается с другими частицами (скажем, с покоящимися электронами), то постепенно он переходит на более низкие уровни, пока наконец не окажется на самом низком (фиг. 223).
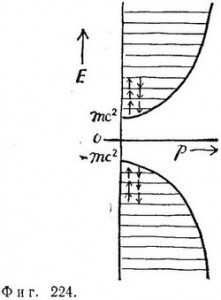
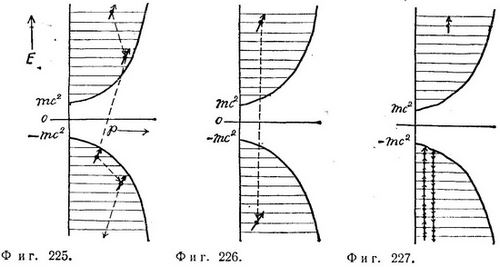
По-иному устроены энергетические уровни электрона Дирака (фиг. 224). Как и раньше, каждому уровню соответствуют два спиновых состояния. Спектр положительных энергий начинается с того места, где энергия равна mс2 (энергия покоя электрона) плюс энергия, которой обладает электрон согласно принципу неопределенности, в силу того, что он заключен в сосуде. Выше этой точки расположены остальные дискретные уровни, удовлетворяющие релятивистскому соотношению между энергией и импульсом; на каждом из этих уровней могут находиться два электрона с противоположно направленными спинами. Принципиально новая особенность этого спектра состоит в наличии уровней с отрицательной энергией. Эти уровни начинаются вблизи—mс2 и простираются вплоть до—∞, зеркально повторяя расположение уровней с положительной энергией, которые начинаются вблизи mс2 и простираются до ∞. Трудность квантовой теории состоит в том, что невозможно изолировать состояния с отрицательной энергией от состояний с положительной энергией; электрон может совершить переход с положительного уровня энергии на уровень с отрицательной энергией, как показано на фиг. 225. В результате электрон, сталкиваясь с другими частицами и теряя энергию, может перейти на уровень с отрицательной энергией и начнет непрерывно ускоряться, а его энергия будет стремиться к —∞.
Чтобы предотвратить возможность катастрофического ускорения электронов, Дирак выдвинул следующее предположение: то, что мы воспринимаем как вакуум, не является на самом деле пустотой, а является системой, в которой на всех отрицательных уровнях находятся по два электрона. В результате, конечно, в вакууме оказывается слишком много электронов (бесконечное число). Таким образом, спектр электрона, находящегося в так называемом пустом пространстве, выглядит совсем не так, как показано на фиг. 226, когда электрон может совершить переход в весьма неуютное состояние с отрицательной энергией, а скорее так, как на фиг. 227, где все отрицательные уровни заполнены другими электронами. Согласно принципу запрета, электрон не может совершить переход на какой-нибудь занятый уже уровень с отрицательной энергией, и поэтому он остается там, где нам хотелось бы его видеть, т. е. на одном из уровней с положительной энергией. Если бы электроны не подчинялись принципу запрета, предположение Дирака потеряло бы всякий смысл. (На этом основана устанавливаемая релятивистской квантовой теорией связь между спином и статистикой, между принципом запрета и состояниями с отрицательной энергией.)
На первый взгляд это предположение вызывает больше вопросов, чем дает ответов. Совершенно неожиданно вакуум превратился из пустоты Демокрита, Гассенди и Ньютона в нечто, напоминающее скорее «plenum» Аристотеля или Декарта. Теперь нельзя уже сказать, что вакуум ничего не содержит. Это очень сложная система, содержащая в некотором смысле половину всего сущего, система, все отрицательные уронил энергии, которой заполнены электронами. (Со временем представление о вакууме несколько изменилось, так что явная асимметрия между заполненными и пустыми уровнями исчезла, однако динамика современного вакуума и его сложность тесно связаны с тем вакуумом, который был впервые предложен Дираком.)
Сразу же возникает несколько очевидных вопросов. Прежде всего каждый электрон обладает зарядом —е, так что бесчисленное количество электронов имело бы бесконечный заряд. Таким образом, предложенный Дираком вакуум, в котором заполнены все уровни с отрицательной энергией, должен обладать бесконечным зарядом. Дирак не отрицает этого. Однако, говорит он, мы воспринимаем этот бесконечный заряд как нормальное состояние вещей. Ощущаем же мы лишь отклонения от этого состояния. Помимо заряда, вакуум должен обладать бесконечной массой и бесконечной отрицательной энергией. Все это, по мнению Дирака, нормальное состояние вещей; воспринимаются лишь отклонения от этого состояния. Хуже другое: электроны, заполняющие отрицательные уровни, образуют сложную силовую систему, так как они электрически взаимодействуют между собой. Поэтому вряд ли пригодны здесь те решения, которые мы выписывали и которые соответствуют свободным электронам, т. е. электронам в отсутствие сил. И снова Дирак не знает ответа, но он говорит: предположим, что результирующая структура уровней примерно такая же, как у свободных частиц.
Если согласиться со всеми этими предположениями, то из них вытекает следующее:
- Можно получить волновые функции, описывающие поведение электрона с произвольным импульсом, который связан с энергией релятивистским соотношением; при этом автоматически получается, что спин электрона равен 1/2, а магнитный момент равен eh/4πmc.
- Динамические свойства такого электрона во многом отвечают тому, что следовало бы ожидать при релятивистском обобщении уравнения Шредингера. Энергия электрона всегда положительна, и электрон может совершать переходы только на уровни с положительной энергией, так как все отрицательные уровни заполнены; в этом отношении он ведет себя вполне нормально.
- Считается, что вакуум — это такое состояние, в котором уровни отрицательной энергии заполнены, а положительной энергии — свободны.
Выясним, однако, что происходит, если электрон, находившийся на уровне с отрицательной энергией, возбуждается и переходит на уровень с положительной энергией. Такой процесс столь же правдоподобен, как и обратный процесс, когда электрон перескакивает с положительного уровня на отрицательный. Если это происходит, то мы имеем электрон с положительной энергией и дырку в уровнях с отрицательной энергией. Как интерпретировать эту дырку?
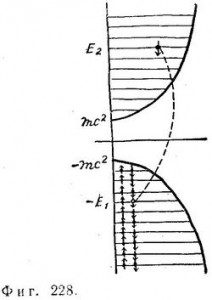
[На фиг. 228 изображен электрон, перескакивающий с отрицательного уровня (—Е1) на уровень с положительной энергией (E2). После перехода энергия равна:
Е2— (—Е1) = Е1 + E2] (47.10)
На том месте, которое мы по привычке называем «пустотой», появляется электрон, находящийся в состоянии с положительной энергией, и отсутствует электрон в состоянии с отрицательной энергией.