Обсудим еще одну характеристику метода — его сложность. Развитие и улучшение компьютерной техники повлекло за собой создание различных алгоритмов, обеспечивающих решение бессчетных прикладных задач, при этом даже для однотипных задач создавалось (и создается) много алгоритмов (программ). Подобные методы ранее были названы эквивалентными. Но для практики недостаточно знать, что решение некой задачки на компьютере в принципе может быть (т.е. неувязка алгоритмически разрешима). Выполнение хоть какого метода просит определенного объема памяти компьютера для размещения данных и программки, также времени центрального микропроцессора по обработке этих данных — эти ресурсы ограничены и, как следует, правомочен вопрос об эффективности их использования. Таким макаром, в самом широком смысле понятие эффективности связано со всеми вычислительными ресурсами, необходимыми для работы метода. Но обычно под «самым эффективным» понимается метод, обеспечивающий более резвое получение результата, так как в практических ситуациях конкретно ограничения по времени нередко являются доминирующим фактором, определяющим пригодность того либо другого метода. По этой причине дальше будет дискуссироваться конкретно временная сложность алгоритмов.
Время работы метода комфортно выражать в виде функции от одной переменной, характеризующей «размер» определенной задачки, т.е. объем входных данных, нужных для ее решения. Таковой подход комфортен, так как сравнительная сложность задач может оцениваться через ее размер. Так как описание задачки, созданной для решения средством вычислительного устройства, можно рассматривать в виде слова конечной длины, представленной знаками конечного алфавита, в качестве формальной свойства размера задачки можно принять длину входного слова. К примеру, если стоит задачка определения наибольшего числа в некой последовательности из n частей, то и размер задачки будет n, так как хоть какой вариант входной последовательности можно задать словом из п знаков.
Временная сложность метода — это функция, которая каждой входной длине слова п ставит в соответствие наибольшее (для всех определенных однотипных задач длиной п) время, затрачиваемое методом на ее решение.
При всем этом, непременно, подразумевается, что во всех задачках употребляется однообразная схема кодировки входных слов.
Разные методы имеют различную временную сложность и выяснение того, какие из их окажутся довольно эффективны, а какие нет, определяется многими факторами. Но теоретики, специализирующиеся разработкой и анализом алгоритмов, для сопоставления эффективности алгоритмов предложили обычный подход, позволяющий прояснить ситуацию. Идет речь о различии меж полиномиальными и экспоненциальными методами.
Полиномиальным именуется метод, временная сложность которого выражается некой полиномиальной функцией размера задачки п. Методы, временная сложность которых не поддается схожей оценке, именуются экспоненциальными.
Различие меж обозначенными 2-мя типами алгоритмов становятся в особенности видными при решении задач огромного размера. Для сравнения в табл. 7.2 приведены данные о времени решения задач различной трудности (данные взяты из книжки М.Гэри, Д.Джонсона [15, с.20] и соответствуют состоянию развития вычислительной техники примерно двадцатилетней давности — это сказывается на абсолютных значениях времени обработки, но относительные характеристики при всем этом не поменяются).
Из приведенных данных видно, что, во-1-х, время обработки экспоненциальных алгоритмов при схожих размерах задач (превосходящих 20) намного выше, чем у полиномиальных; во-2-х, скорость нарастания времени обработки с повышением размера задачки у экспоненциальных алгоритмов существенно выше, чем у полиномиальных.
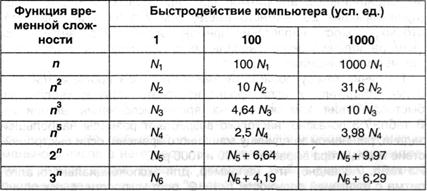
Различие меж обоими типами алгоритмов появляются еще больше внушительно, если проанализировать воздействие роста быстродействия компьютера на время выполнения метода. В табл. 7.3 показано, как растут размеры большей задачки, решаемой за единицу машинного времени, если быстродействие компьютера вырастет в 100 и 1000 раз.
Из табл. 7.3 видно, что, к примеру, для экспоненциального метода с функцией трудности f(n) = 2n рост скорости вычислений в 1000 раз приводит только к тому, что размер большей задачки растет всего на 10 единиц, в то время как для функции f(n) = п5 она растет практически в 4 раза.
Таблица 7.2.
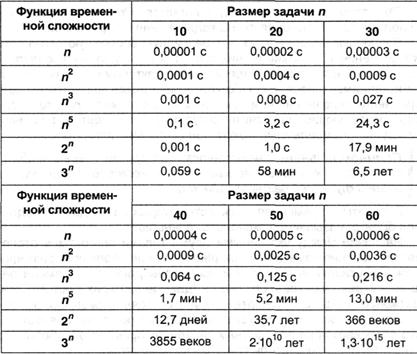

Таблица 7.3.

Приведенные примеры призваны показать, что подобно тому, как есть алгоритмически неразрешимые задачки, есть и задачки беспристрастно сложные, т.е. такие, трудозатратность которых нереально уменьшить совершенствованием компьютера. Задачка считается труднорешаемой, если для нее не удается выстроить полиномиального метода. Это утверждение не является категорическим, так как известны задачки, в каких довольно отлично работают и экспоненциальные методы. Примером может служить симплекс-метод, который удачно применяется при решении задач линейного программирования, имея функцию трудности f(n) = 2n. Но схожих примеров не сильно много, и общей следует признать ситуацию, что отлично исполняемыми можно считать полиномиальные методы с функциями трудности п, n2 либо п3. К примеру, при решении задачки поиска подходящего данного из п имеющихся в худшем варианте сложность равна п; если же оценить среднюю трудозатратность (длительность поиска), то она составит (п + 1)/2 — в обоих случаях функция трудности оказывается линейной п. Задачка ранжирования, т.е. расстановки в данном порядке п однотипных данных приводит к полиному 2-й степени; сложность задачки вычисления определителя системы п линейных уравнений с п неведомыми характеризуется полиномом 3-й степени. Увеличение быстродействия частей компьютера уменьшает время выполнения метода, но не уменьшает степень полинома трудности. Как следует, решению практической задачки на компьютере должна предшествовать оценка ее трудности и подтверждение того, что задачка решаема за применимое время.
