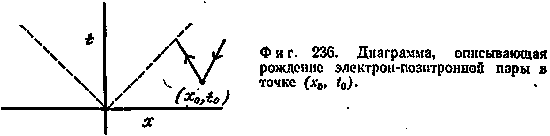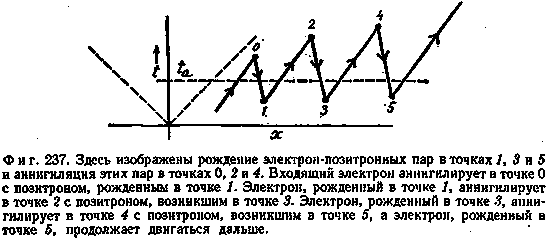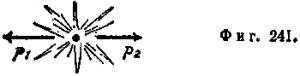Говорят, Лагранж страшно гордился тем, что его «Аналитическая механика», помимо прочих достоинств, обладала еще тем достоинством, что в ней не было ни одного чертежа. Использование рисунков вместо тысяч слов облегчило (если не сделало вообще возможной) жизнь современному поколению физиков и внесло существенные упрощения в расчеты бухгалтерского типа, необходимые для исследования взаимодействий между релятивистскими квантами.
Такое событие, как, например, рождение электрон-позитронной пары, можно представить на диаграмме, где этот процесс происходит в определенной пространственно-временной точке. Так как три направления в пространстве обладают одинаковыми свойствами, вместо них можно условно говорить об одном направлении, которое принято обозначать буквой х; ось времени — обычно ось ординат — принято обозначать буквой t. Тогда такое событие, как рождение электрон-позитронной пары, изобразится диаграммой, представленной па фиг. 235. На этой диаграмме отдельно указаны электрон и позитрон, так как они являются различными частицами. Однако, поскольку считается, что позитрон — это просто отсутствие электрона на уровне с отрицательной энергией, то при желании можно рассматривать позитрон (что и делал Фейнман) как электрон с отрицательной энергией, движущийся вспять во времени. Выражение «электрон с отрицательной энергией, движущийся вспять во времени» звучит довольно дико, однако формально смысл этого выражения весьма прост. Под ним подразумевается, что если в уравнении, описывающем движение электрона с отрицательной энергией, заменить t на —t, в результате чего время будет идти не вперед, а назад, то позитрон, движущийся вперед во времени, будет обладать свойствами электрона с отрицательной энергией, но движущегося во времени в обратном направлении. Это довольно причудливое свойство уравнения движения позволяет перерисовать показанную на фиг. 235 диаграмму таким образом, что электрон и позитрон не будут отличаться между собой ничем, кроме направлений стрелок (фиг. 236).
Теперь не нужно отмечать электрон и позитрон отдельными подписями, так как мы договорились, что частица, движущаяся вспять во времени, является позитроном, или античастицей электрона. В общем случае античастицы всех частиц со спином 1/2 представляются как исходные частицы с отрицательной энергией, движущиеся во времени в обратном направлении.
Если теперь проследить за электронной линией, не обращая внимания, куда движется электрон — вперед или вспять во времени, то мы сразу же убедимся в полезности нового метода рассмотрения. Ибо электронная линия всегда остается одной электронной линией; она никогда не раздваивается. Она может идти вперед во времени, описывая электрон, или назад, описывая позитрон, но одна линия всегда остается одной линией (фиг. 237). Например, в момент ta имеются четыре электрона и три позитрона. Число электронов минус число позитронов равно 1; эта разность не изменяется. В момент ta ситуация кажется весьма сложной. Если же рассматривать ее, прослеживая ход электронной линии, то она выглядит довольно простой. Электрон движется вспять во времени от точки 0 до точки 1, вперед во времени от 1 до 2, вспять во времени от 2 до 3 и т. д. Однако имеется всего лишь одна линия, поэтому мы видим, как если бы мы обладали зрением всевышнего, который способен обозревать все пространство и время на одном полотне, что весь процесс вызывается единственным электроном, движущимся то вперед, то назад во времени.
Пространственно-временные диаграммы оказываются особенно полезными при исследовании взаимодействия между электронами и фотонами. В теории тяготения Ньютона сила, действующая, например, между Солнцем и планетой, зависит только от расстояния между этими телами и обладает природой, совершенно отличной от природы тел, на которые она действует. В релятивистской квантовой теории (квантовой теории поля) взаимодействие между двумя телами происходит всегда в результате обмена тел квантами того же или иного поля. Иными словами, кванты влияют на движение квантовых частиц, обменивающихся между собой другими квантами. Последние, согласно теории относительности, не могут двигаться со скоростью, превышающей скорость света; это объясняет, почему действие одного тела на другое проявляется не мгновенно, а через конечный промежуток времени. Фундаментальное взаимодействие электрона с электромагнитным полем, которое является для него самым сильным и наиболее существенным из всех взаимодействий, можно изобразить с помощью диаграммы, представленной па фиг. 238.
На всех предыдущих диаграммах было показано рождение электрон-позитронной пары из ничего или превращение ее в ничто; однако в природе такие процессы не происходят. Если в вакууме рождается электрон-позитронная пара или если она аннигилирует, то, как правило, такие процессы происходят в результате взаимодействия электронов и позитронов с фотонами, так как фотон — квант электромагнитного поля — есть частица, сильнее всего взаимодействующая с электронами и позитронами. На фиг. 239 изображена диаграмма, описывающая процесс аннигиляции электрона и позитрона.
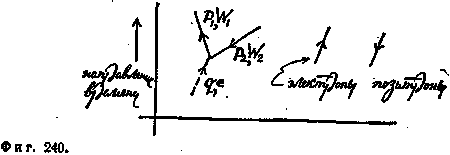
Часто удобнее характеризовать эти процессы не пространственно-временными координатами, а энергией и импульсом. (Если процесс характеризуется только пространственно-временными координатами, то соответствующие энергия и импульс являются полностью неопределенными; если же он характеризуется энергией и импульсом, то нельзя уже говорить о точном значении его пространственно-временных координат, а можно лишь указывать направление времени, чтобы различать частицы и античастицы.) На фиг. 240 изображена диаграмма рождения фотоном электрон-позитронной пары, которая характеризуется приведенными на фигуре значениями энергии и импульса.
На этой диаграмме процесс описывается импульсом q и энергией ɛ падающего фотона, импульсом p1 и энергией W1 вылетающего электрона и импульсом — р2 и энергией W2 вылетающего позитрона. Согласно принятой нами бухгалтерской системе расчетов, в вершинах диаграмм такого типа импульс должен сохраняться, т. е. импульс входящих частиц должен равняться импульсу выходящих из вершины частиц:
q+p2=p1.
Энергия же может при этом не сохраняться. Она должна сохраняться лишь в том случае, когда процесс происходит реально, т. е. когда мы действительно наблюдаем рождение фотоном в вакууме электрон-позитронной пары. Различие между реальным и виртуальным процессами состоит в том, что виртуальный процесс в отличие от реального является просто вспомогательным орудием наших расчетов. Реальный же процесс действительно происходит в природе и удовлетворяет всем законам сохранения. Используя релятивистские соотношения, связывающие энергию и импульс фотона, электрона и позитрона, можно показать, что в вершине, изображенной на фиг. 240, энергия и импульс не могут одновременно сохраняться; именно поэтому фотон не может, согласно квантовой теории поля, самопроизвольно породить электрон-позитронную пару в вакууме. Чтобы это произошло, вблизи фотона должна находиться заряженная частица, которая поглотила бы избыток энергии или импульса.
Поясним, почему в вершине диаграммы нельзя добиться одновременного сохранения энергии и импульса. В системе центра масс (фиг. 241) вылетающих частиц (мы можем наблюдать движение из любой инерциальной системы отсчета, так как в данном случае принцип относительности выполняется) должно быть:
p1 + p1 = 0,
причем энергия частиц больше 2mc2; ясно, однако, что не существует фотона, импульс которого равен нулю, а энергия больше 2mc2, так как для фотона:
Е=ср. (48.2)
Поэтому одновременно не могут выполниться два закона сохранения:
При вычислении амплитуды процесса с помощью теории возмущений полная амплитуда представляется в виде суммы членов (как будет описано ниже), однозначно соответствующих вершинам рассмотренного выше типа. Совершенно не обязательно, чтобы энергия сохранялась в каждой из этих вершин. Тем самым мы различаем подобные виртуальные, или промежуточные, процессы (являющиеся подсобным аппаратом и возникающие только в рамках используемого нами математического метода и выполняющие подсобную роль) и так называемые реальные процессы, в которых энергия сохраняется.