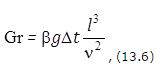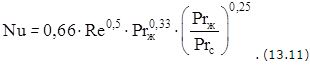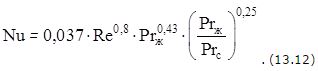Теория подобия — это учение о подобии явлений. Наиболее простое подобие — геометрическое. У геометрически подобных фигур — сходственные стороны пропорциональны, а соответственные углы равны.
Понятие подобия распространяется на любые физические явления, например подобие движения двух потоков жидкости или подобие распределения температур и тепловых потоков.
Подобие физических явлений возможно только при качественно одинаковых явлениях, которые описываются одинаковыми уравнениями. Если же физическое содержание различно, но явления описываются одинаковыми уравнениями, то эти явления называются аналогичными. Например, процессы теплопроводности и электропроводности.
При этом подобие физических явлений означает подобие всех величин, характеризующих рассматриваемые явления. Обязательной предпосылкой подобия физических явлений должно быть подобие геометрическое.
Из анализа математического описания подобных процессов установлены критерии подобия, которые для подобных явлений сохраняют одно и то же числовое значение. Критерии подобия — это безразмерные комплексы, составленные из величин, характеризующих явление. Критерии подобия названы именами ученых внесших существенный вклад в развитие науки.
Основные положения теории подобия формулируются в виде трех теорем.
Первая теорема подобия — подобные между собой процессы имеют одинаковые критерии подобия.
Вторая теорема — зависимость между переменными, характеризующими процесс, может быть представлена в виде зависимости между критериями подобия. Эта теорема дает возможность обобщать и представлять данные эксперимента в виде критериальных зависимостей.
Третья теорема подобия — подобны те процессы, критерии которых численно одинаковы. Эта теорема отвечает на вопрос: какие условия необходимы и достаточны чтобы процессы были подобны. При изучении процессов теплообмена пользуются критериями определяемыми и определяющими. В процессах теплообмена в качестве определяемого выступает критерий Нуссельта, характеризующий интенсивность процесса конвективного теплообмена
Nu = αl/λ (13.4)
Здесь a — коэффициент теплоотдачи, Вт/(м2·град);
l — характерный размер стенки (размер, участвующий в процессе, для круглой трубы — d), м;
l — коэффициент теплопроводности среды, омывающей твердую стенку, Вт/(м·град).
Как известно, интенсивность теплообмена зависит от условий омывания твердой стенки жидкостью. Условия омывания определяются характером движения — вынужденной или естественной конвекцией. Вынужденная конвекция характеризуется критерием Рейнольдса, естественная конвекция — критерием Грасгофа. Соответственно определяющим критерием при вынужденной конвекции является критерий Рейнольдса
Re = V*d/v, (13.5)
где V — скорость движения потока жидкости, м/с;
d — характерный размер (при движении внутри труб — внутренний диаметр d), м;
n — кинематическая вязкость текущей жидкости, м2/с.
Критерий Грасгофа, который характеризует интенсивность подъемной силы в этих условиях естественной конвекции:
где b — температурный коэффициент объемного расширения среды, здесь β = 1/Т;
Т — абсолютная температура среды, К;
g — ускорение свободного падения, g = 9,81 м/с2;
Dt — разность температур между температурой греющей стенки и температурой среды;
l — характерный размер. Для горизонтальной трубы — d, для вертикальной трубы — высота трубы h;
n — кинематическая вязкость среды, м2/с.
Кроме критериев Re и Gr в теплотехнических расчетах в качестве определяющего принимает участие критерий Прандтля, который характеризует теплофизические свойства теплоносителя.
Pr = v/α, (13.7)
где n — кинематическая вязкость теплоносителя, м2/с;
a — коэффициент температуропроводности, м2/с.
Таким образом, при вынужденном движении теплообмен зависит от режима движения и теплофизических параметров теплоносителя Nu = ƒ(Re, Pr), а при естественной конвекции Nu = ƒ(Gr, Pr).
На практике встречаются случаи, когда одновременно с вынужденным движением на теплообмен большое влияние оказывает и свободная конвекция и тогда Nu = ƒ(Re, Gr, Pr). Причем влияние естественной конвекции будет тем больше, чем меньше скорость вынужденного потока и чем выше разность температур между стенкой и жидкостью.
В процессе теплообмена меняется температура жидкости, и, следовательно, меняются значения физических свойств жидкости. Как правильно выбрать температуру, по которой будут определяться значения физических параметров? Для этого введено понятие определяющей температуры, при значении которой из таблиц находят величины вязкости, теплопроводности и значение критерия Прандля Pr.
Однозначной рекомендации по выбору определяющей температуры нет. Распространен выбор в качестве определяющей — средней температуры жидкости. Пользуются также значениями, средней температуры стенки (теплообменной поверхности), температуры жидкости на входе в аппарат, и т.д. Универсального способа выбора температур нет. Поэтому целесообразно в качестве определяющей принимать такую, которая либо задана в расчетах, либо легко определяется.
Важен также вопрос выбора определяющего размера, хотя с точки зрения теории подобия любой размер может быть принят в качестве определяющего. Целесообразно выбрать размер, который определяет развитие процесса теплообмена. Например, при теплообмене внутри трубы, определяющий размер — внутренний диаметр трубы, при поперечном обтекании трубы — наружный диаметр, при обтекании плиты — ее длина по направлению движения, при теплообмене в кольцевом зазоре — разность диаметров. Для каналов неправильной формы применяется формула определения эквивалентного диаметра:
dэкв = 4F/П, (13.8)
где F — площадь поперечного сечения канала, м2;
П — периметр канала, м.
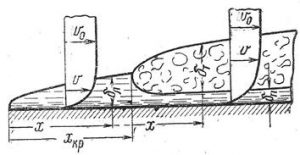
Течение жидкости вдоль пластины, после накатывания потока на край пластины, сопровождается образованием гидродинамического пограничного слоя. В нем скорость движения жидкости изменяется от нуля на поверхности пластины, к которой прилипают частички жидкости, до значения скорости невозмущённого потока V0 — на внешний границе этого пограничного слоя (рис. 13.1).
Рис. 13.1. Схема движения жидкости при обтекании пластины
Образование пограничного слоя и падение скорости в нем происходят из-за вязкости жидкости. У передней кромки в начале пластины толщина пограничного слоя минимальна, затем она растет, ее величина зависит от расстояния от передней кромки и степени турбулизации набегающего потока. При небольшой турбулизации потока движение жидкости вдоль пластины сопровождается увеличением толщины пограничного слоя, тормозящее воздействие стенки распространяется на всё более далекие слои жидкости. Режим движения в пограничном слое ламинарный, толщину слоя на расстоянии x от начала пластины можно рассчитать по формуле
δл = 5x / Re0,5. (13.9)
Однако при значительной турбулизации набегающего потока, когда Re > 105, в пограничном слое, на некотором критическом расстоянии xкр начинают возникать вихри, и течение жидкости в слое приобретает турбулентный характер. В пограничном слое начинается перемешивание жидкости, которое всё-таки затухает поблизости от поверхности пластины — здесь сохраняется очень тонкий вязкий подслой, изображенный в правой половине рис. 13.1. Толщина турбулентного пограничного слоя также возрастает пропорционально удалению от начального края пластины
δT = 0,37x / Re0,2. (13.10)
При разности температур пластины и набегающего потока между поверхностью пластины и жидкостью возникает теплообмен. Величину удельного теплового потока можно вычислить по формуле Ньютона (13.1) Тепловой поток пропорционален температурному напору (tс — tж), и коэффициенту теплоотдачи, который зависит от гидродинамической картины и режима течения теплоносителя, расстояния x от передней кромки и от теплофизических свойств теплоносителя.
Около поверхности пластины в потоке жидкости, кроме гидродинамического, формируется также тепловой пограничный слой, в пределах которого температура теплоносителя изменяется от tс до tж. Температуру tс имеют частицы жидкости, прилипшие к стенке, температура tж характерна для жидкости, находящейся вдали от поверхности стенки. Характер распределения температур в тепловом пограничном слое зависит от режима движения жидкости в динамическом пограничном слое. Формирование теплового пограничного слоя сходно с характером развития гидродинамического слоя.
При ламинарном пограничном слое перенос тепла в слое осуществляется только за счет теплопроводности.
При турбулентном динамическом слое основное изменение температуры происходит в пределах тонкого вязкого подслоя около поверхности теплообмена. В турбулентном ядре пограничного слоя из-за интенсивного перемешивания жидкости изменение температуры незначительно.
Увеличение разности температур (tс — tж) усложняет процесс, так как изменяются теплофизические параметры теплоносителя. Изменение вязкости, теплопроводности и температуропроводности сказывается на интенсивности теплоотдачи. Например, при охлаждении жидкости (тепловой поток направлен от жидкости к стенке) наиболее интенсивно снижается температура в пограничном слое жидкости, а значит вязкость пограничного слоя возрастает, что приводит к утолщению пограничного слоя, уменьшению скорости в нем, а следовательно, и к уменьшению теплоотдачи.
Коэффициент теплоотдачи при ламинарном режиме течения теплоносителя можно определить из критериального уравнения:
Для определения среднего коэффициента теплоотдачи в условиях турбулентного режима жидкости вдоль пластины рекомендуется зависимость:
В формулах (3.11) и (3.12):
Prж — критерий Прандтля теплоносителя при его средней температуре;
Prс— критерий Прандтля теплоносителя при температуре стенки.
Nu = α*l/λ;
Re = V*l/v,
где l — длина пластины, обтекаемой потоком жидкости, м;
a — средний коэффициент теплоотдачи, Вт/(м2·град);
V — средняя скорость движения потока жидкости, м/с;
l — средняя теплопроводность жидкости при ее средней температуре, Вт/мК;
n — вязкость жидкости, м2/с.
Множитель Prж/Prc представляет собой поправку, учитывающую направление теплового потока. Если жидкость нагревается в результате процесса теплообмена, то Prж/Prc > 1, а при охлаждении жидкости Prж/Prc < 1.
Если в качестве теплоносителя используется воздух, или двухатомные газы, то формулы (13.11) и (13.12) упрощаются, так как значение критерия Прандтля для воздуха в широком диапазоне температур практически неизменно и поправка Prж/Prc = 1.
Уравнения (3.11) и (3.12) трансформируются для воздуха в выражения:
Nu = 0,57Re0,5; (13.111)
Nu = 0,032Re0,8. (13.121)