Максвелл открыл путь, который со временем превратился в широкую столбовую дорогу. В течение последующих ста лет было воздвигнуто грандиозное здание статистической механики, в частности благодаря работам Людвига Больцмана и Дж. Вилларда Гиббса. (Гиббс был первым великим американским физиком-теоретиком, который, как и другие «пророки», был признан в собственном университете в последнюю очередь. Говорят, что президент Йельского университета, решив создать физический факультет, обращался за помощью к нескольким европейским ученым. Они отсылали его к Вилларду Гиббсу, которого президент не знал. Гиббс в это время числился в штате Йельского университета.)
Суть статистической гипотезы, сформулированной для газов, состоит в том, что мы отказываемся от попыток узнать точное положение и скорость каждой из множества частиц, образующих систему, а вместо этого предполагаем, если нет никакой дополнительной информации, что для каждой частицы системы все возможные положения и направления скорости равновероятны (следует особо подчеркнуть слово равновероятны). Некоторую информацию мы все-таки имеем: предполагается, что полная энергия системы Е и полное число частиц в ней N фиксированы (мы считаем, что энергия и число частиц сохраняются). Поэтому некоторые комбинации скоростей и положений совокупности частиц запрещены; в качестве примера запрещенной системы укажем такую комбинацию, когда хотя бы одна частица обладает энергией, большей Е: в таком случае полная энергия системы превышала бы Е.
Можно было бы представить себе ситуацию, когда вся энергия газа вложена в одну частицу, которая движется с чрезвычайно большой скоростью, соответствующей энергии Е, а остальные частицы стоят неподвижно. Мы чувствуем, однако, что такая конфигурация вряд ли «жизнеспособна», так как можно ожидать, что быстро движущаяся частица будет сталкиваться с другими частицами и отдавать им при этом часть своей энергии. Возможна и другая комбинация, когда полная энергия газа поделена поровну между всеми молекулами, которые движутся равным строем одна за другой с одинаковыми скоростями; но и эта ситуация, как подсказывает нам интуиция, выглядит маловероятной, так как столкновения приведут в конце концов к хаотизации движения.
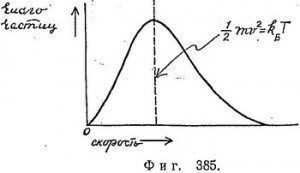

Рассмотрим все возможные (и различающиеся между собой) распределения молекул в пространстве и по скоростям, удовлетворяющие условиям, что энергия Е и число частиц N остаются неизменными, когда все молекулы находятся в одном углу сосуда и имеют одну скорость, когда они находятся в другом углу и имеют другую скорость и т. д., т. е. примем во внимание абсолютно все возможные комбинации. Найдем теперь наиболее вероятное распределение положений и скоростей молекул. Эта задача при перечисленных выше условиях разрешима. Основная идея статистики заключена в гипотезе, что, если система находится при заданной температуре (в тепловом равновесии, как, например, газ в сосуде), скорости и положения молекул описываются наиболее вероятным распределением. Зная это наиболее вероятное распределение молекул, можно вычислить коэффициент вязкости, давление и другие величины.
Распределение Максвелла — Больцмана требует, чтобы частицы были однородно распределены в пространстве, а их скорости — как показано на фиг. 385. Это и есть наиболее вероятное распределение частиц по положениям и скоростям при условии, что все конфигурации равновероятны, а полное число частиц и их полная энергия фиксированы.


Таким образом, мы обходимся без допущения о равенстве скоростей частиц и не решаем уравнений движения, из которых мы могли бы получить точные значения координат и скоростей каждой частицы, но вводим наиболее вероятное распределение по положениям в пространстве и по скоростям для всех частиц. Это весьма радикальное предположение выходит далеко за рамки законов механики, недаром его долго и интенсивно обсуждали, и анализировали уже после Максвелла и Больцмана. Это допущение формулировали по-разному. Но по существу все сводится к чисто интуитивной догадке, что в любой реальной физической ситуации маловероятные распределения молекул (как по пространству, так и по скоростям) не могут возникать настолько часто, чтобы оказывать хоть какое-то влияние на равновесные свойства системы.
Проиллюстрируем смысл этой гипотезы на нескольких примерах. Рассмотрим газ, состоящий из большого числа частиц, заключенных в сосуде. Вполне возможно такое распределение частиц, когда все частицы движутся в одну сторону, ударяются в какой-то момент об одну стенку сосуда и ни одна из них не ударяется о противоположную стенку (фиг. 386). В результате такого движения к одной стенке сосуда будет приложена значительная сила, а на другую стенку сила действовать не будет, поэтому весь сосуд отскочит вбок, пока противоположная стенка не столкнется с молекулами, после чего сосуд отскочит назад. Это возможно, но маловероятно. Вряд ли 1023 молекул смогут на мгновение упорядочить свое движение и начать двигаться в одном направлении вместо того, чтобы беспорядочно метаться во все стороны.


Может также случиться, что в какой-то момент все молекулы вдруг очутятся в одном углу сосуда, а все другие части сосуда окажутся пустыми (фиг. 387). В это мгновение плотность газа в одном углу сосуда станет очень большой, тогда как в других его частях плотность будет равна нулю. Такая ситуация тоже возможна, но маловероятна.
Предположим, что на автомобильной стоянке находится 10 000 машин й стоянка, имеет лишь один выезд; когда заканчивается футбол, все владельцы машин садятся за руль. Спрашивается: возможна ли такая ситуация, когда все машины непрерывным потоком выедут со стоянки, не образуя «пробок» или скоплений машин в некоторых местах? Конечно, это возможно, но крайне маловероятно, если на месте не окажется, большого количества дорожных полицейских. Как правило же, при, освобождении стоянки образуется немыслимая каша из машин, поскольку каждая из них перемещается почти случайным образом, пытаясь выехать со стоянки.
Предположение, содержащееся в работах Максвелла, Больцмана и Гиббса, равнозначно утверждению, что большое количество частиц, подчиняющихся ньютоновским законам движения, при наличии тех или иных внешних ограничений (например, постоянства полной энергии и полного числа частиц) в результате, взаимных соударений в конечном итоге переходят в некое среднее состояние. Из знаменитой теоремы Больцмана (H-теоремы) следует, что при заданных начальных условиях столкновения частиц приводят, к постепенному установлению наиболее вероятного состояния. Статистическая механика избавляет, нас от всех неудобств, связанных с решением уравнений движения. Она основывается на предположении, что распределение частиц в равновесном состоянии является наиболее вероятным, и выводит затем все следствия, вытекающие из этого распределения. Очевидно, что могут возникать и такие распределения, которые не являются наиболее вероятными. Не менее очевидно, однако, что такие распределения быстро исчезнут, если потрясти сосуд или ввести беспорядок каким-либо иным способом.
